离散数学2期末复习

函数

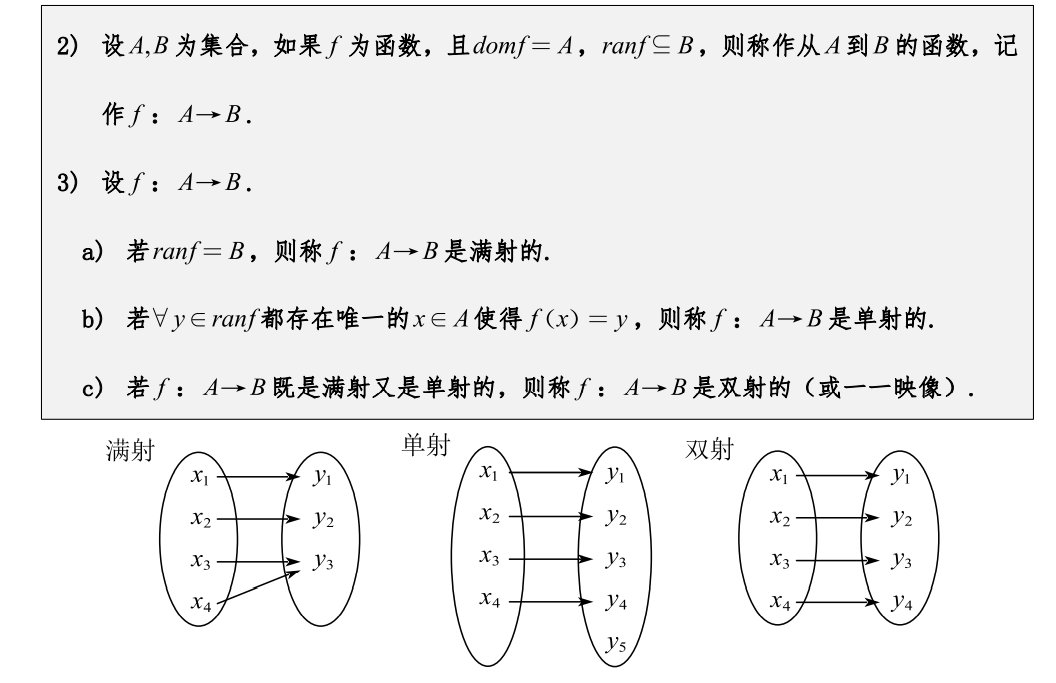
函数及其性质的判断、函数值、像、原像等的计算

• 满射：subjective

• 单射：ingective

• 双射：bijective

• 像是函数值的集合

函数的复合及反函数

顺序不要反了

集合基数的概念

略

图

• 阶：顶点数
• 度：顶点作为端点的次数
• 零图：一条边都没有的图
• 平凡图：只有一个点的图

握手定理

• 度数之和等于边数的两倍 $ l = 2m$
• 入度之和=出度之和=边数
• 奇度顶点的个数是偶数

可图化条件

1. 度数之和 $l$ 为偶数
2. 最大度小于等于 $n-1$ （你一个点最多也就把其他点连一遍）

无向完全图

• 每个点都与剩余点连接，记作 $K_{n}$ （ $n$ 为阶数）
• 边点条数为 $\dfrac{n\left( n-1\right) }{2}$

图的连通性

图的矩阵表示

关联矩阵

邻接矩阵

可达矩阵

Dj

树

$m=n-1$

• 中序：左中右
• 前序：中左右
• 后续：左右中

几种特殊的图

欧拉图

通过所有边一次

• 无向图充要：连通无奇度
• 有向图充要：强连通、每个点入度等于出度

哈密顿图

通过所有点一次

注意是充分条件不是充要 $d\left( u\right) +d\left( v\right) \geq n-1$

二部图与平面图

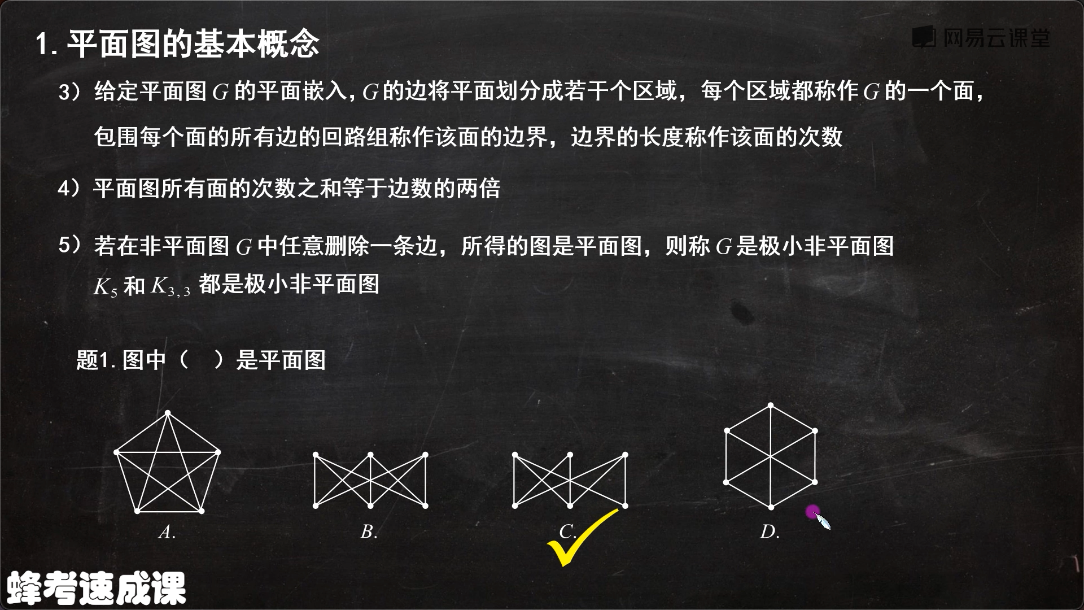
• 欧拉公式：$n-m+r=2$
• 面数之和等于边数两倍

• 平面图的必要：$m\leq 3n-6$

基本的组合计数公式

1. 排列公式：$A_n^k=\frac{n!}{(n-k)!}$，表示从 $n$ 个不同的元素中选出 $k$ 个元素进行排列的方案数。

   $n$ 开始往后递减相乘 $k$ 个数

2. 组合公式：$C_n^k=\frac{n!}{k!(n-k)!}$，表示从 $n$ 个不同的元素中选出 $k$ 个元素进行组合的方案数。

3. 重复排列公式：$n^k$，表示从 $n$ 个不同的元素中选出 $k$ 个元素进行重复排列的方案数。

4. 重复组合公式：$C_{n+k-1}^k$，表示从 $n$ 个不同的元素中选出 $k$ 个元素进行重复组合的方案数。

• 二项式定理 $$(x+y)^n=\sum_{k=0}^n {n\choose k}x^ky^{n-k}$$

递推方程、生成函数及应用

递推方程

具体来说，假设方程的一般形式为 $ax^3+bx^2+cx+d=0$，其导数为 $f'(x)=3ax^2+2bx+c$。如果 $f'(x)$ 的根与原方程的一个根相同，则说明这个根是重根。

更具体地，可以使用以下的判断方法：

1. 求出方程的三个根 $x_1,x_2,x_3$。
2. 求出方程的导数 $f'(x)$。
3. 求出导数 $f'(x)$ 的两个根 $y_1,y_2$。
4. 判断 $y_1$ 是否等于 $x_1$、$x_2$ 或 $x_3$，或者判断 $y_2$ 是否等于 $x_1$、$x_2$ 或 $x_3$。如果有任意一个条件成立，则说明方程有重根。

需要注意的是，如果 $f'(x)$ 的两个根都与方程的某个根相同，则这个根是二重根；如果有三个根都相同，则这个根是三重根。

生成函数

直接放弃

代数系统

• 交换 Commutative
• 结合 Assciative
• 幂等 Idempotent
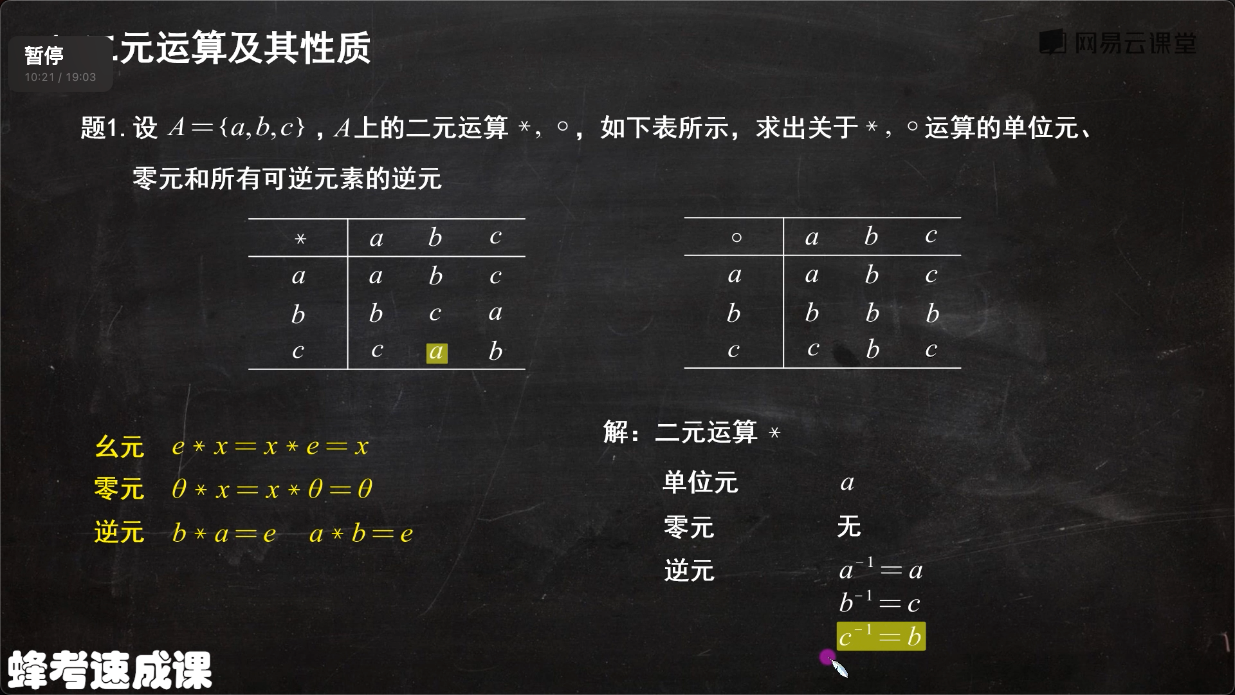
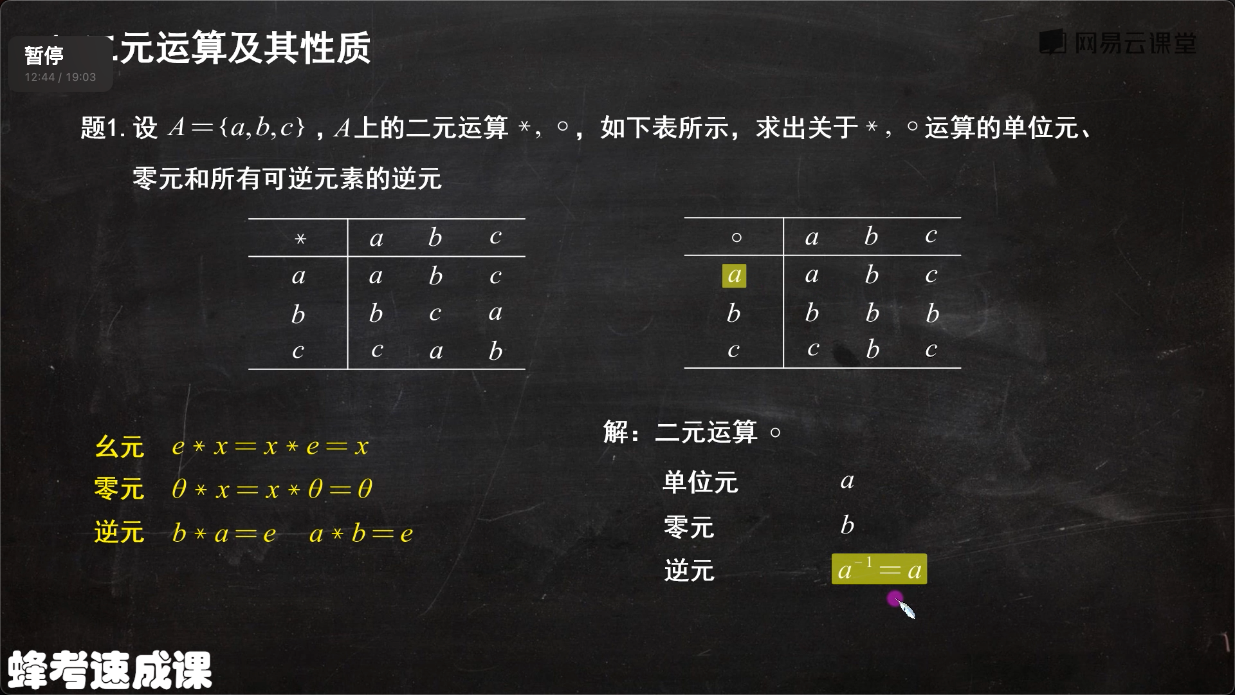
• 幺元 Identity
• 零元 Zero element
• 逆元 Inverse element